Sinc Interpolation

At some point, I think it’s safe to say that every individual studying digital signal processing wondered how a digital signal (which is discrete/sample-based) was able to accurately represent a sound wave which is continuous.

It turns out that, apart from the quantization errors introduced during the sampling process, we can accurately reconstruct our continuous analog signal using sinc interpolation.
Here is the sinc function:

\[\begin{align} \DeclareMathOperator{\sinc}{sinc} \sinc(x) &= \dfrac{\sin(\pi x)}{\pi x} \end{align}\]

I made a graph¹ that shows the original signal (dark grey), the interpolated signal (blue), as well as the sinc functions centered and scaled at every sample (random colours).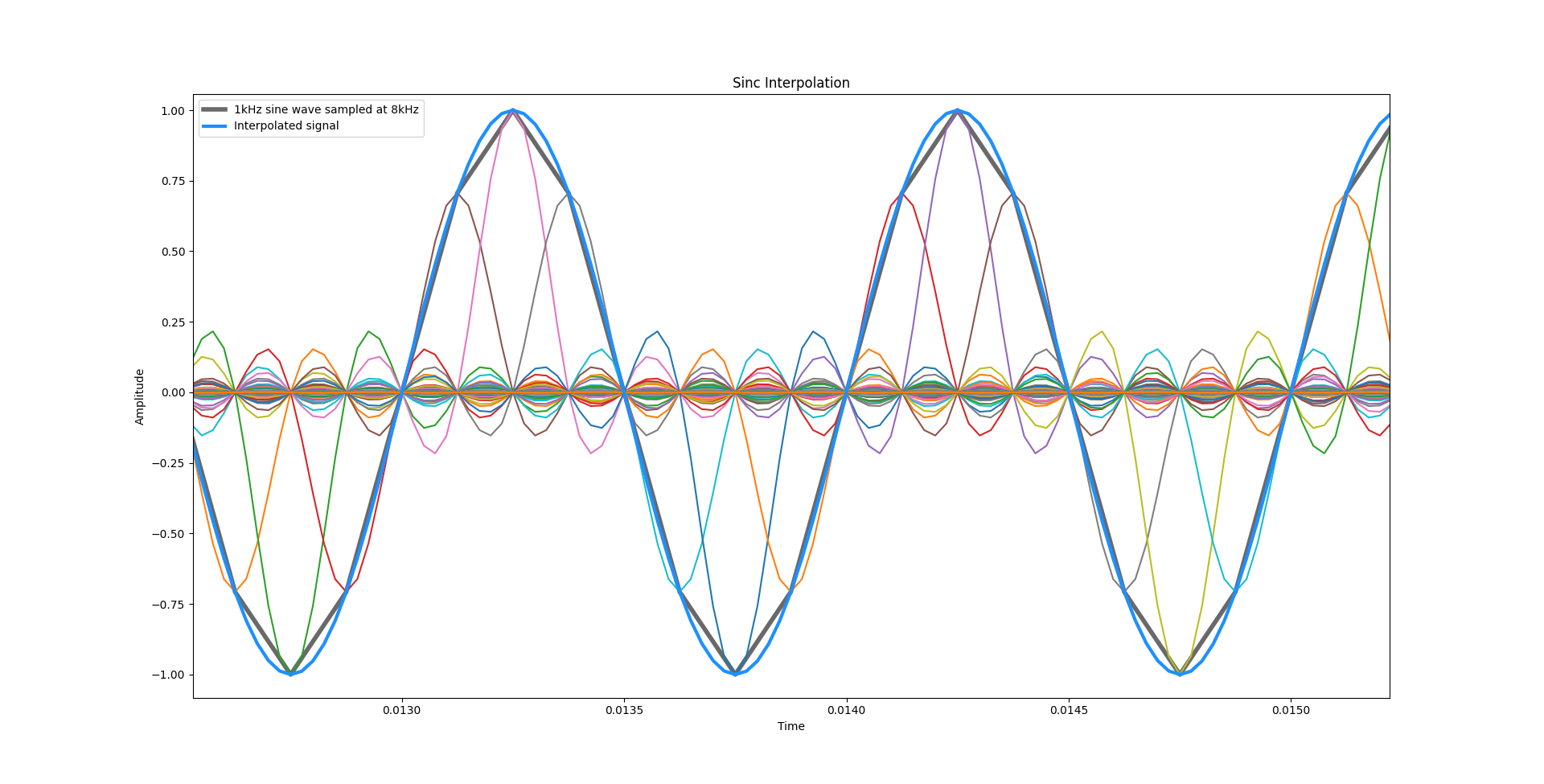

If we interpolate using continuous sinc functions centered and scaled at every sample of our digital signal and then sum everything (this is also known as convolution), we get an accurate reconstruction of our continuous signal.
This property is useful if we want to upsample (like we did in the example) and also when converting to the analog domain, which works with continuous signals.

---

1. In this example, the interpolated signal is still a digital signal since we are still working in the digital domain. ↩︎